Skip to contents

2-Arm, Time-To-Event Outcome - Analysis

Anoop Singh Rawat and Shubham Lahoti

June 04, 2025

2ArmTimeToEventOutcomeAnalysisDescription.Rmd

Introduction

The following examples illustrate how to integrate new analysis capabilities into East Horizon or East using R functions in the context of a two-arm trial. In each example, the trial design includes a standard-of-care control arm and an experimental treatment arm, with patient outcomes modeled as time-to-event data. The design includes two interim analyses (IA) and one final analysis (FA). At each IA, an analysis is conducted which may lead to early stopping for efficacy or futility, depending on the predefined design criteria.

Once CyneRgy is installed, you can load this example in RStudio with the following commands:

CyneRgy::RunExample( "2ArmTimeToEventOutcomeAnalysis" )

Running the command above will load the RStudio project in RStudio.

RStudio Project File: 2ArmTimeToEventOutcomeAnalysis.Rproj

In the R directory of this example you will find the following R files:

  1. AnalyzeUsingEastLogrankFormula.R - Contains a function named AnalyzeUsingEastLogrankFormula to demonstrate the R code necessary for Example 1 as described below.
  2. AnalyzeUsingSurvivalPackage.R - Contains a function named AnalyzeUsingSurvivalPackage to demonstrate the R code necessary for Example 2 as described below.
  3. AnalyzeUsingHazardRatioLimitsOfCI.R - Contains a function named AnalyzeUsingHazardRatioLimitsOfCI to demonstrate the R code necessary for Example 3 as described below.

Example 1 - Using Formulas Q.242 and Q.243 from the East manual

In this example, the analysis is customized by replacing the default method with a user-defined calculation based on formulas of the Appendix Q.8 - Survival : Two Samples from the East manual (Q.242 and Q.243).

Numerator of Test Statistic:

Num=∑i=1MWi⋅Numi\text{Num} = \sum_{i=1}^M W_i \cdot \text{Num}_i

With:

Numi=di,t−ni,t⋅dini\text{Num}_i = d_{i,t} - n_{i,t} \cdot \frac{d_i}{n_i}

Where:

  • Wi=1W_i = 1 is the weight for the Logrank Test.
  • di,td_{i,t} and di,cd_{i,c} are the numbers of events at time tit_i in the treatment and control groups, respectively.
  • ni,tn_{i,t} and ni,cn_{i,c} are the numbers of subjects at risk just before time tit_i in the treatment and control groups, respectively.
  • di=di,t+di,cd_i = d_{i,t} + d_{i,c} is the total number of events at time tit_i.
  • ni=ni,c+ni,cn_i = n_{i,c} + n_{i,c} is the total number of subjects at risk just before time tit_i.

Denominator of Test Statistic:

Den=∑i=1MWi2⋅Deni\text{Den} = \sum_{i=1}^MW_i^2 \cdot \text{Den}_i

With:

Deni=ni,t⋅ni,c⋅(ni−di)⋅dini2⋅(ni−1)\text{Den}_i = \frac{n_{i,t} \cdot n_{i,c} \cdot (n_i - d_i) \cdot d_i}{n_i^2 \cdot (n_i - 1)}

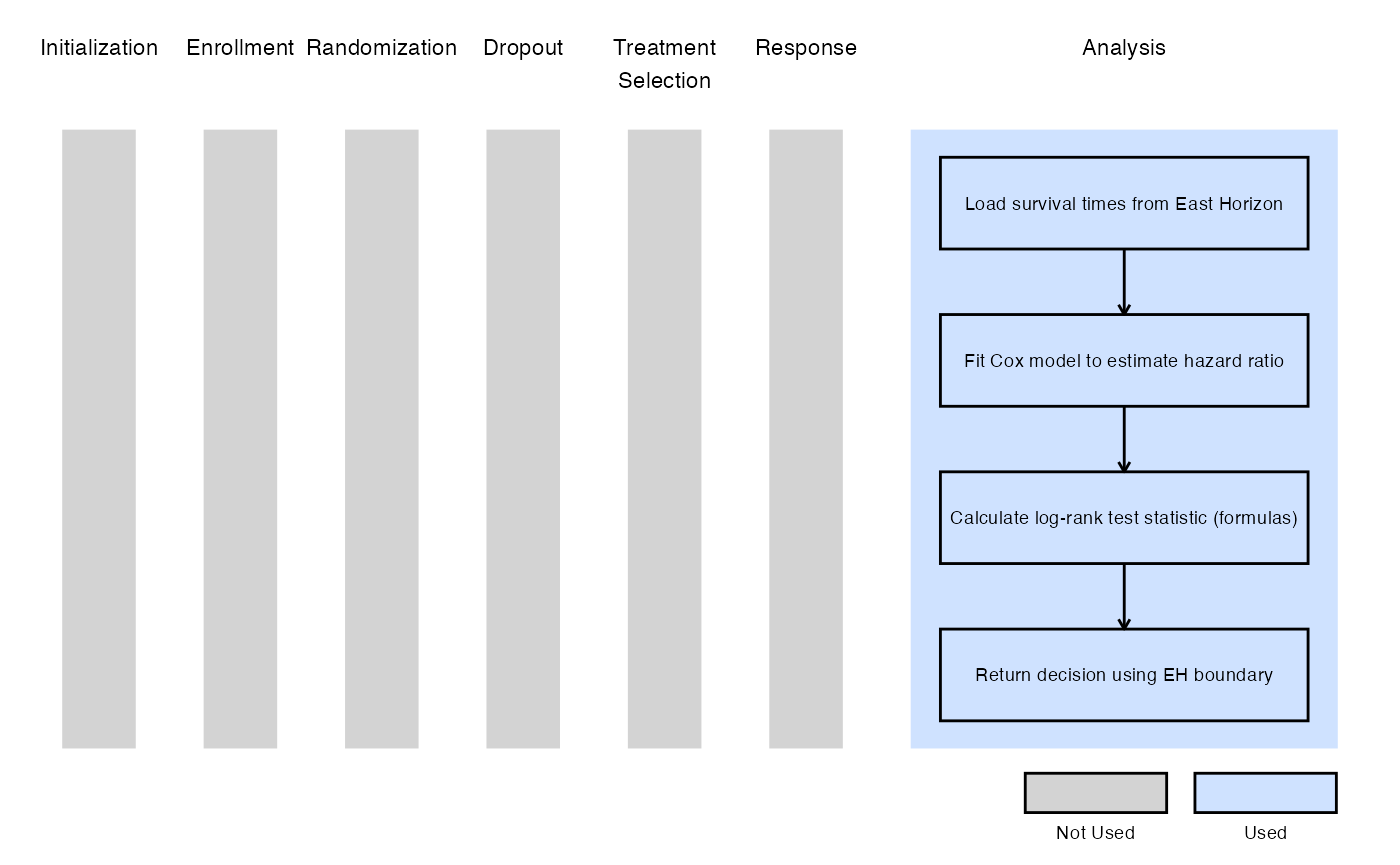
The objective is to demonstrate a straightforward way to modify both the analysis and decision-making process. The computed test statistic is compared to the efficacy boundary provided by East Horizon or East as input. This example does not include a futility rule and does not use any user-defined parameters.

The figure below illustrates where this example fits within the R integration points of Cytel products, accompanied by a flowchart outlining the general steps performed by the R code.

Example 2 - Using the survival::survdiff() Function

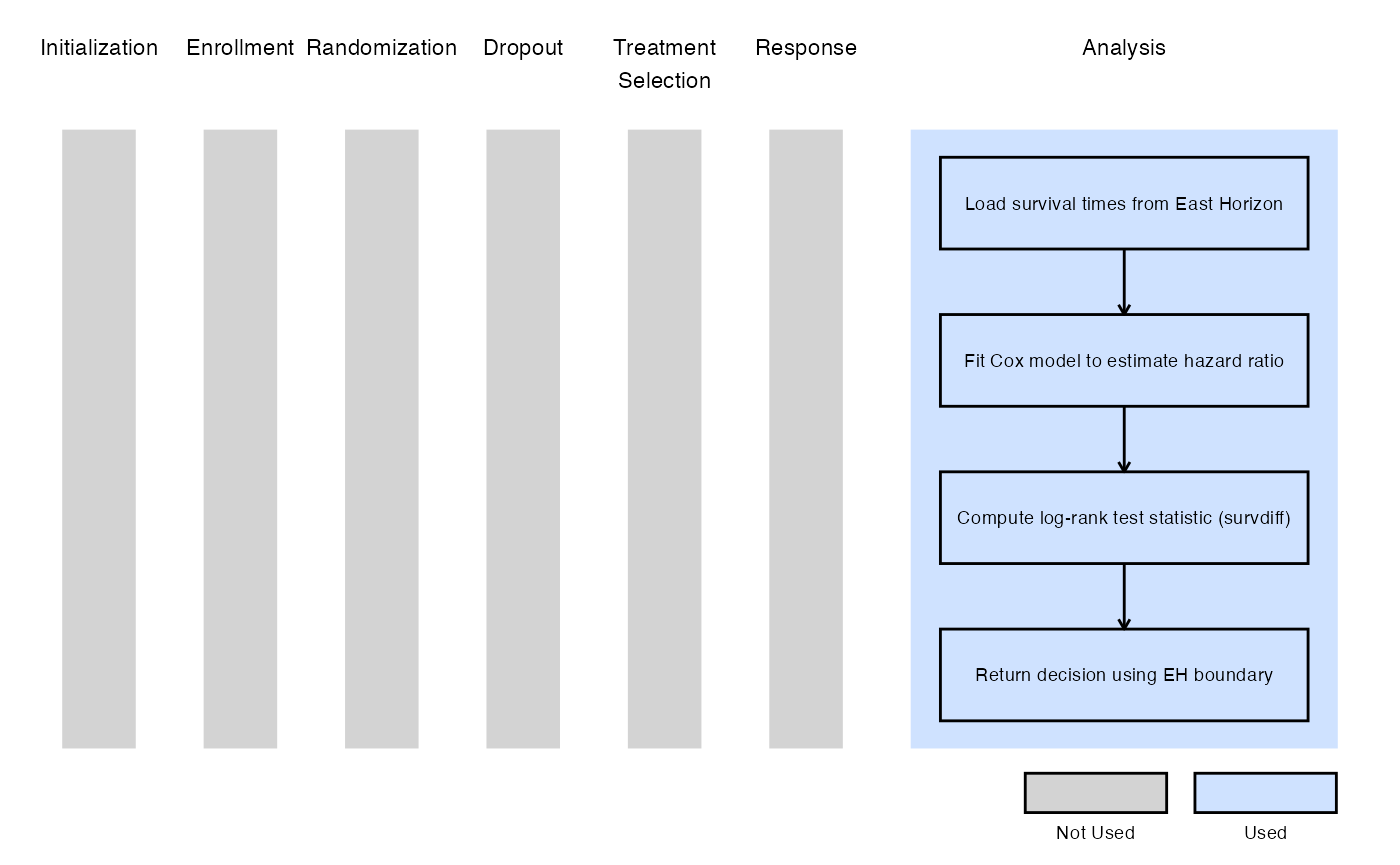
This example utilizes the survival::survdiff() function from the survival package to perform the log-rank test. The resulting chi-square statistic is used to compute the log-rank value, which is then compared to the lower efficacy boundary provided by East Horizon or East. Like Example 1, this example does not include a futility rule and does not use any user-defined parameters.

The figure below illustrates where this example fits within the R integration points of Cytel products, accompanied by a flowchart outlining the general steps performed by the R code.

Example 3 - Utilization of Confidence Interval Limits for Go/No-Go Decision-Making

In many Phase II trials, Go/No-Go decisions are made based on whether a treatment shows sufficient promise to justify further development. These decisions are often guided by two key thresholds:

  • Minimum Acceptable Value (MAV): The smallest treatment effect (e.g., hazard ratio) considered meaningful.
  • Target Value (TV): A highly desirable treatment effect based on clinical or strategic considerations.

This example demonstrates how to approximate probabilistic decision-making using frequentist confidence intervals (CIs), ignoring the boundaries provided by East Horizon or East in favor of a CI-based logic. If the hazard ratio is likely to be below the MAV, a Go decision is made. If not, and it is unlikely to be below the TV, a No-Go decision is made.

We use the Cox proportional hazards model via the survival::coxph() function to estimate the log hazard ratio (log HR) and its standard error. Based on these estimates, frequentist CIs are constructed to inform decision-making. Specifically:

At Interim Analysis

  • Let LL and UL be the lower and upper limits of the confidence interval for the log HR.
  • If UL<log(MAV)→GoUL < \log(\text{MAV}) \rightarrow \text{Go}
  • If LL>log(TV)→No-GoLL > \log(\text{TV}) \rightarrow \text{No-Go}
  • Otherwise →\rightarrow Continue to the next analysis

At Final Analysis

  • If UL<log(MAV)→GoUL < \log(\text{MAV}) \rightarrow \text{Go}
  • Otherwise →\rightarrow No-Go

Refer to the table below for the definitions of the user-defined parameters used in this example.

User parameter Definition
dMAV Minimum Acceptable Value: the smallest treatment effect considered clinically meaningful to warrant further development.
dTV Target Value: the desired treatment effect that would represent a strong clinical benefit or strategic advantage.
dConfLevel Confidence Level: the level of confidence used to construct the confidence interval for Go/No-Go decision-making (e.g., 0.80 for an 80% CI).

Note: In this example, the boundary information that is computed in East Horizon or East is ignored. User-defined parameters and the Cox model are used to analyze the data and compute the desired confidence intervals.

The figure below illustrates where this example fits within the R integration points of Cytel products, accompanied by a flowchart outlining the general steps performed by the R code.