
Integration Point: Multiplicity Adjustment
Gabriel Potvin
February 19, 2026
IntegrationPointMultiplicityAdjustment.RmdGo back to the Getting Started: Overview page
Description
The Multiplicity Adjustment integration point allows you to customize how multiple hypotheses are adjusted for Type I error control, instead of relying on East Horizon’s default Fixed Sequence or Fallback methods. For example, you could implement alternative strategies such as Bonferroni, Holm, Hochberg, or graphical approaches.
Availability
East Horizon Explore
This integration point is available in East Horizon Explore for the following study objectives and endpoint types:
| Time to Event | Binary | Continuous | Continuous with repeated measures | Count | Composite | Dual TTE-TTE | Dual TTE-Binary | |
|---|---|---|---|---|---|---|---|---|
| Two Arm Confirmatory | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ✅ | ✅ |
| Multiple Arm Confirmatory | ❌ | ❌ | ❌ | - | - | - | - | - |
| Dose Finding | - | - | ❌ | - | - | - | - | - |
Legend
| Icon | Meaning |
|---|---|
| ✅ | Available |
| ❌ | Not available |
| 🔜 | Coming soon |
East Horizon Design
Click to expand/collapse
This integration point is available in East Horizon Design for the following study objectives and endpoint types:
| Time to Event | Binary | Continuous | Continuous with repeated measures | Count | Composite | Dual TTE-TTE | Dual TTE-Binary | |
|---|---|---|---|---|---|---|---|---|
| Two Arm Confirmatory | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | 🔜 | 🔜 |
| Two Arm Confirmatory - Multiple Endpoints | ❌* | ❌* | ❌* | - | - | - | - | - |
| Multiple Arm Confirmatory | ❌ | ❌ | ❌ | - | - | - | - | - |
| Dose Finding | - | - | ❌ | - | - | - | - | - |
*For Multiple Endpoints, you can use the Integration Point: Design to implement your own multiplicity method.
This integration point is available in East Horizon Design for the following tests:
| Test | Study Objective | Endpoint | Availability |
|---|---|---|---|
| Single Mean (One Arm Design) | One Arm Exploratory/Confirmatory | Continuous | ❌ |
| Mean of Paired Differences (Paired Design) | One Arm Exploratory/Confirmatory | Continuous | ❌ |
| Mean of paired Ratios (Paired Design) | One Arm Exploratory/Confirmatory | Continuous | ❌ |
| Single Proportion (One Arm Design) | One Arm Exploratory/Confirmatory | Binary | ❌ |
| Simon’s Two Stage (One Arm Design) | One Arm Exploratory/Confirmatory | Binary | ❌ |
| Logrank Weibull Distribution (One Arm Design) | One Arm Exploratory/Confirmatory | Time to Event | ❌ |
| Parametric Weibull Distribution (One Arm Design) | One Arm Exploratory/Confirmatory | Time to Event | ❌ |
| Logrank Exponential Distribution (One Arm Design) | One Arm Exploratory/Confirmatory | Time to Event | ❌ |
| Single Poisson Rate (One Arm Design) | One Arm Exploratory/Confirmatory | Count | ❌ |
| Difference of Means (Parallel Design) | Two Arm Confirmatory | Continuous | ❌ |
| Ratio of Means (Parallel Design) | Two Arm Confirmatory | Continuous | ❌ |
| Difference of Means (Crossover Design) | Two Arm Confirmatory | Continuous | ❌ |
| Ratio of Means (Crossover Design) | Two Arm Confirmatory | Continuous | ❌ |
| Difference of Proportions (Parallel Design) | Two Arm Confirmatory | Binary | ❌ |
| Ratio of Proportions (Parallel Design) | Two Arm Confirmatory | Binary | ❌ |
| Odds Ratio of Proportions (Parallel Design) | Two Arm Confirmatory | Binary | ❌ |
| Fisher’s Exact (Parallel Design) | Two Arm Confirmatory | Binary | ❌ |
| Logrank Test Given Accrual Duration and Accrual Rates (Parallel Design) | Two Arm Confirmatory | Time to Event | ❌ |
| Logrank Test Given Accrual Duration and Study Duration (Parallel Design) | Two Arm Confirmatory | Time to Event | ❌ |
| Logrank Test Given Accrual Duration and Accrual Rates (Population Enrichment) | Two Arm Confirmatory | Time to Event | ❌ |
| Ratio of Poisson Rates (Parallel Design) | Two Arm Confirmatory | Count | ❌ |
| Ratio of Negative Binomial Rates (Parallel Design) | Two Arm Confirmatory | Count | ❌ |
| Win Ratio (Parallel Design) | Two Arm Confirmatory | Composite | ❌ |
| MAMS Difference of Means (Pairwise Comparisons to Control) | Multiple Arm Confirmatory | Continuous | ❌ |
| MAMS Difference of Means: Combining P-Values (Pairwise Comparisons to Control) | Multiple Arm Confirmatory | Continuous | ❌ |
| MAMS Difference of Proportions (Pairwise Comparisons to Control) | Multiple Arm Confirmatory | Binary | ❌ |
| MAMS Difference of Proportions: Combining P-Values (Pairwise Comparisons to Control) | Multiple Arm Confirmatory | Binary | ❌ |
| MAMS Logrank (Pairwise Comparisons to Control) | Multiple Arm Confirmatory | Time to Event | ❌ |
| MAMS Logrank: Combining P-Values (Pairwise Comparisons to Control) | Multiple Arm Confirmatory | Time to Event | ❌ |
Instructions
In East Horizon Explore
You can set up a multiplicity adjustment function under Multiplicity Adjustment in a Design Card while creating or editing an Input Set.
Follow these steps (click to expand/collapse):
- Select User Specified-R from the dropdown in the Multiplicity Adjustment field in the Design Card.
- Browse and select the appropriate R file (
filename.r) from your computer, or use the built-in R Code Assistant to create one. This file should contain function(s) written to perform various tasks to be used throughout your Project. - Choose the appropriate function name. If the expected function is not displaying, then check your R code for errors.
- Set any required user parameters (variables) as needed for your function using + Add Variables.
- Continue creating your project by specifying scenarios for patient Response, Enrollments, etc.
For a visual guide of where to find the option, refer to the screenshot below:
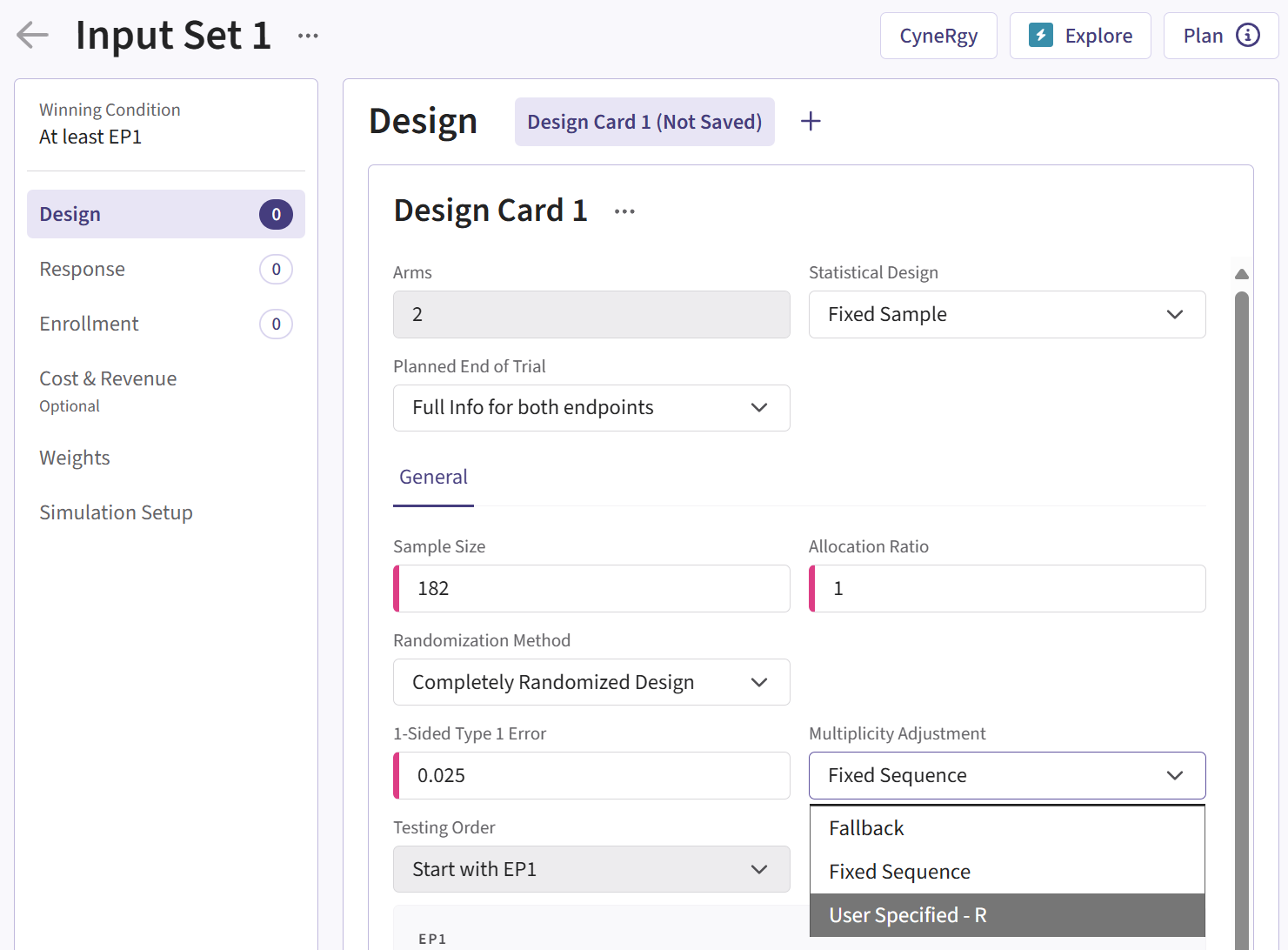
Input Variables
When creating a custom R script, you can optionally use specific
variables provided by East Horizon’s engine itself. These variables are
automatically available and do not need to be set by the user, except
for the UserParam variable. Refer to the table below for
the variables that are available for this integration point, outcome,
and study objective.
| Variable | Type | Description |
|---|---|---|
| SimData | Data Frame | Subject data generated in current simulation, one row per subject.
To access these variables in your R code, use the syntax:
SimData$NameOfTheVariable, replacing
NameOfTheVariable with the appropriate variable name. See
below for more information. |
| DesignParam | List | Input parameters which may be needed to compute test statistics and
perform tests. To access these variables in your R code, use the syntax:
DesignParam$NameOfTheVariable, replacing
NameOfTheVariable with the appropriate variable name. See
below for more information. |
| LookInfo | List | Input parameters related to multiple looks. Empty when
Statistical Design = Fixed Sample, but still mandatory in
the functions CyneRgy::GetDecisionString and
CyneRgy::GetDecision. See below for more information. |
| TestStat | Named List of Numeric | Named List of length equal to the number of endpoints, indicating
the value of the test statistic on Wald ﴾Z﴿ scale for each endpoint. For
example, TestStat[“Endpoint 1”] is the test statistic for
Endpoint 1. This is returned by the Analysis part. |
| OutList | List | List of outputs that was returned in the previous look. Only
relevant for Statistical Design = Group Sequential. Set to
NULL for the first look. See below in the Output
Variable. |
| UserParam | List | Contains all user-defined parameters specified in the East Horizon
interface (refer to the Instructions
section). To access these parameters in your R code, use the syntax:
UserParam$NameOfTheVariable, replacing
NameOfTheVariable with the appropriate parameter name. |
Note: “Endpoint 1” is used as a sample endpoint name. It will be the actual endpoint name as specified by the user.
Expected Output Variable
East Horizon expects an output of a specific type. Refer to the table below for the expected output for this integration point:
| Output | Type | Description |
|---|---|---|
| Decision | Vector of Integer | Vector of length DesignParam$NumTreatments, containing
the boundary crossing decision for each treatment arm:– 0: No boundary crossed.– 1: Lower efficacy
boundary crossed.– 2: Upper efficacy boundary
crossed.– 4: Futility boundary crossed (only applicable
when Statistical Design = Group Sequential). |
| OutList | List | List of outputs to pass to the next look. Only relevant for
Statistical Design = Group Sequential. Will be available as
input to this function in the next look. See above in the Input
Variables. |
| ErrorCode | Integer | Optional. Can be used to handle errors in your script: – 0: No error.– Positive Integer: Nonfatal
error, the current simulation will be aborted, but the next simulation
will proceed.– Negative Integer: Fatal error, no
further simulations will be attempted. |
Minimal Template
Your R script could contain a function such as this one, with a name
of your choice. All input variables must be declared, even if they are
not used in the script. We recommend always declaring
UserParam and OutList as a default
NULL value in the function arguments, as this will ensure
that the same function will work regardless of whether the user has
specified any custom parameters in the interface and whether or not
OutList is used.
A detailed template with step-by-step explanations is available here: Decision.DEP.R
For Statistical Design = Fixed Sample
PerformMultAdj <- function( SimData, DesignParam, TestStat, OutList = NULL, UserParam = NULL )
{
nError = 0 # Error handling (no error)
Decision = list()
Decision[ EndpointName[[ 1 ]]] = 0 # Initialize decision for endpoint 1
Decision[ EndpointName[[ 2 ]]] = 0 # Initialize decision for endpoint 2
# Write the actual code here.
return( list( Decision = as.list( Decision ), ErrorCode = as.integer( nError )))
}For Statistical Design = Group Sequential
PerformMultAdj <- function( SimData, DesignParam, LookInfo, TestStat, OutList = NULL, UserParam = NULL )
{
nError = 0 # Error handling (no error)
Decision = list()
Decision[ EndpointName[[ 1 ]]] = 0 # Initialize decision for endpoint 1
Decision[ EndpointName[[ 2 ]]] = 0 # Initialize decision for endpoint 2
OutList = list()
OutList$OutVal = 0 # This value will be passed to the next look
# Write the actual code here.
return( list( Decision = as.list( Decision ), OutList = as.list( OutList ), ErrorCode = as.integer( nError )))
}